学习笔记——分块、线段树

AI摘要
加载中...
摘要由AI自动生成，仅供参考！

继续备赛CSP-S，这次解决一下此前让人只有我闻之色变的线段树。

当然，在此之前，先来看看比较简单的分块。

不过在此之前，先理一理这两种数据结构（？）的适用范围。

（注：本文是对于OI WIKI即其它内容写作而来的学习笔记，内容可能稍显一致，但绝非抄袭/洗稿等，欢迎对比）

分块

具体而言，分块并不是数据结构，而是一种思想。

在一次同时以相同操作处理大量数据时，不单独处理而进行统筹操作，一次性完成处理。

这使得其可以用于快速计算类似区间和的问题。

比之线段树其更为简单，当然，随数据量上升而渐进的复杂度就是相应的代价。

不过在数据量不大时显然分块更能帮助我们快速解决问题。

原理

想象我们有一组共nn个数据，记为x0x_0到xn−1x_{n-1}。

现在，我们希望得到[a,b]\left[ a,b \right]范围内的区间和。

如果线性存储，那么对于每次询问操作，都需要进行(b−a+1)\left( b-a+1 \right)次求和，是O(n)O\left( n \right)级别的时间复杂度。

于是开始分块。将数据分为每yy个一组，记为z0z_0到zny−1z_{\frac{n}{y}-1}（其中zi=∑j=iyiy+y−1xjz_i=\sum_{j=iy}^{iy+y-1}{x_j}）[1]：

x0,x1,x2,x3,...,xy−1⏟z0,xy,xy+1,.⏟z1,z2.....,xn−1⏟zny−1\underset{z_0}{\underbrace{x_0,x_1,x_2,x_3,...,x_{y-1}}},\underset{z_1,z_2...}{\underbrace{x_y,x_{y+1},.}}.\underset{z_{\frac{n}{y}-1}}{\underbrace{.,x_{n-1}}}

此时，对于[a,b]\left[ a,b \right]的区间和，可以很容易想到求法（一般而言最后一块不会是完整块，不过无伤大雅）：

  • 若xax_a与xbx_b在同一块内，遍历xax_a到xbx_b求和。
  • 若xax_a与xbx_b不在同一块内，区间和为∑i=aayy+y−1xi+∑i=ay+1by−1zi+∑i=byybxi\sum_{i=a}^{\frac{a}{y}y+y-1}{x_i}+\sum_{i=\frac{a}{y}+1}^{\frac{b}{y}-1}{z_i+\sum_{i=\frac{b}{y}y}^b{x_i}}，即包含了xax_a与xbx_b的不完整块与中间的完整块。

只要在建块的时候进行预处理就可以通过分块节省大量时间（单次操作时间复杂度变为O(ny+y)O\left( \frac{n}{y}+y \right)）

利用基本不等式a+b⩾2aba+b\geqslant 2\sqrt{ab}可以得知，当且仅当ny=y\frac{n}{y}=y时，(ny+y)\left( \frac{n}{y}+y \right)取最小值2n2\sqrt{n}。也就是说，当每个块大小为n\sqrt{n}时，单次操作得到最小时间复杂度O(n)O\left(\sqrt{n} \right)。

于是我们可以尝试开始建块。

建块

首先，定义数据结构：

1
2
3
4
5
6
7
8
template <class T>
class blocks {
	vector<T> datas;
	vector<T> sums;
	size_t s;

	//...
};

用向量存储数据，用s来存储每一块的大小。

然后，建块：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//...
class blocks {
	//...
	
	void build(vector<T> d, size_t ss) {
		size_t length = d.size();
		
		datas.clear();
		sums.clear();
		datas.resize(length);
		
		T sum = 0;
		size_t cnt = 0;
		for(size_t i = 0;i < length;i++) {
			datas[i] = d[i];
			sum += d[i];
			cnt++;
			if(cnt == ss) {
				sums.push_back(sum);
				cnt = 0;
				sum = 0;
			}
		}
		if(cnt != 0) sums.push_back(sum);
		
		s = ss;
	}

	//...
};

在建块时计算每一块的区间和并存储即可（别忘了可能有的不完整块）。

以及根据由基本不等式得到的结论，块大小s一般为size_t(sqrt(d.size()))

对于求区间和操作，依照原理一节所述操作即可。

如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//...
class blocks {
	//...

    public:
        T query(size_t begin, size_t end) {
            size_t block_begin = begin / s;
            size_t block_end = end / s;

            T sum = 0;

            //在同一块里吗？
            if(block_begin == block_end) {
                //如果在，线性遍历求和即可
                for(size_t i = begin;i <= end;i++) {
                    sum += datas[i];
                }

                return sum;
            }

            //如果不在，分别计算左、中、右三部分
            //左
            for(size_t i = begin;i < (block_begin + 1) * s;i++) {
                sum += datas[i];
            }

            //右（注意小于等于）
            for(size_t i = block_end * s;i <= end;i++) {
                sum += datas[i];
            }

            //中
            for(size_t i = block_begin + 1;i < block_end;i++) {
                sum += sums[i];
            }

            return sum;
        }

	//...
};

更改

存入了数据后，我们自然希望能够自由地更改存入的数据。

对于区间内的修改操作，同样分为两类（以修改区间[a,b]\left[ a,b\right]为例）：

  • 若xax_a与xbx_b在同一块内，遍历xax_a到xbx_b赋值（需要重新计算区间和）。
  • 若xax_a与xbx_b不在同一块内，遍历包含了xax_a与xbx_b的两个不完整块赋值（同上），以及修改中间完整块的区间和即可（无需修改数据本身，具体内容如下代码）。

问题在于，修改了包含数个整块的数据的值以后，计算修改范围内的完整块内的区间和时可能会导致结果未正确更新。此时需要引入新结构：懒惰标记（lazy marker）。

对每一个块建立懒惰标记，在查询时通过懒惰标记累计增量更新即可。

所以我们有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
template <class T>
class blocks {
	vector<T> datas;
	vector<T> sums;
	vector<T> lazy_markers; //引入懒惰标记
	size_t s;

	void build(vector<T> d, size_t ss) {
		size_t length = d.size();
		
		datas.clear();
		sums.clear();
		lazy_markers.clear(); //清空懒惰标记
		datas.resize(length);
		
		T sum = 0;
		size_t cnt = 0;
		for(size_t i = 0;i < length;i++) {
			datas[i] = d[i];
			sum += d[i];
			cnt++;
			if(cnt == ss) {
				sums.push_back(sum);
				lazy_markers.push_back(0); //与sums一一对应
				cnt = 0;
				sum = 0;
			}
		}
		if(cnt != 0) {
			sums.push_back(sum);
			lazy_markers.push_back(0); //同理，与sums一一对应
		}
		
		s = ss;
	}

    public:
        T query(size_t begin, size_t end) {
            size_t block_begin = begin / s;
            size_t block_end = end / s;

            T sum = 0;

            if(block_begin == block_end) {
                for(size_t i = begin;i <= end;i++) {
                    sum += datas[i] + lazy_marker[block_begin]; //增加懒惰标记内的增量
                }

                return sum;
            }

            for(size_t i = begin;i < (block_begin + 1) * s;i++) {
                sum += datas[i] + lazy_marker[block_begin]; //增加懒惰标记内的增量
            }

            for(size_t i = block_end * s;i <= end;i++) {
                sum += datas[i] + lazy_marker[block_end]; //增加懒惰标记内的增量
            }

            for(size_t i = block_begin + 1;i < block_end;i++) {
                sum += sums[i];//区间和已被改变，无需考虑增量
            }

            return sum;
        }

	//...
};

由此，对于增量，我们可以有：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//...
class blocks {
	//...

    public:
		//...

		void update(size_t begin, size_t end, T value) {
            //在同一块里吗？
            if(block_begin == block_end) {
                //如果在，线性遍历更新即可
                for(size_t i = begin;i <= end;i++) {
                    datas[i] += value;
                    sums[block_begin] += value; //更新区间和
                }

                return;
            }

			//如果不在，分别更新左、中、右部分
			//左
			for(size_t i = begin;i < (block_begin + 1) * s;i++) {
				datas[i] += value;
				sums[block_begin] += value; //更新区间和
			}

            //右（注意小于等于）
            for(size_t i = block_end * s;i <= end;i++) {
                datas[i] += value;
                sums[block_end] += value; //更新区间和
            }

            //中
            for(size_t i = block_begin + 1;i < block_end;i++) {
                sums[i] += value * s; //更新区间和
                lazy_marker[i] += value; //更新懒惰标记
            }
		}

	//...
};

比较

当我们希望得到区间最小/最大值时，同样可以采取分块的思想。

相信根据懒惰标记的方法也能想到，只需要再添加两个向量用于维护区间最小/最大值即可。

原理仍然一致，这里不重复给出。

以下是完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
template <class T>
class blocks {
	vector<T> datas;
	vector<T> sums;
	vector<T> lazy_markers;
    vector<T> maxs; //维护区间最大值
    vector<T> mins; //维护区间最小值
	size_t s;

	void build(vector<T> d, size_t ss) {
		size_t length = d.size();

		datas.clear();
		sums.clear();
		lazy_markers.clear();
        maxs.clear();
        mins.clear();
		datas.resize(length);

		T sum = 0;
		size_t cnt = 0;
        T max_val = numeric_limits<T>::min(); //当作负无穷
        T min_val = numeric_limits<T>::max(); //当作正无穷
		for(size_t i = 0; i < length; i++) {
			datas[i] = d[i];
			sum += d[i];
            max_val = max(max_val, d[i]);
            min_val = min(min_val, d[i]);
            cnt++;
			if(cnt == ss) {
				sums.push_back(sum);
				lazy_markers.push_back(0);
                maxs.push_back(max_val);
                mins.push_back(min_val);
                max_val = numeric_limits<T>::min();
                min_val = numeric_limits<T>::max();
				sum = 0;
                cnt = 0;
			}
		}
		if(cnt != 0) {
			sums.push_back(sum);
			lazy_markers.push_back(0);
            maxs.push_back(max_val);
            mins.push_back(min_val);
		}

		s = ss;
	}

    public:
	    //构造函数
        blocks(const vector<T>& d, size_t ss) {
            build(d, ss);
        }

		//query不变

        void update(size_t begin, size_t end, T value) {
            size_t block_begin = begin / s;
            size_t block_end = end / s;

            //重新计算最大/最小值
            T max_val = numeric_limits<T>::min();
            T min_val = numeric_limits<T>::max();

            if(block_begin == block_end) {
                for(size_t i = begin; i <= end; i++) {
                    datas[i] += value;
                    sums[block_begin] += value;
                    max_val = max(max_val, datas[i]);
                    min_val = min(min_val, datas[i]);
                }
                //更新最大/最小值
                maxs[block_begin] = max(maxs[block_begin], max_val);
                mins[block_begin] = min(mins[block_begin], min_val);
                return;
            }

            for(size_t i = begin; i < (block_begin + 1) * s; i++) {
                datas[i] += value;
                sums[block_begin] += value;
                max_val = max(max_val, datas[i]);
                min_val = min(min_val, datas[i]);
            }
            maxs[block_begin] = max(maxs[block_begin], max_val);
            mins[block_begin] = min(mins[block_begin], min_val);

            max_val = numeric_limits<T>::min();
            min_val = numeric_limits<T>::max();
            for(size_t i = block_end * s; i <= end; i++) {
                datas[i] += value;
                sums[block_end] += value;
                max_val = max(max_val, datas[i]);
                min_val = min(min_val, datas[i]);
            }
            maxs[block_end] = max(maxs[block_end], max_val);
            mins[block_end] = min(mins[block_end], min_val);

            for(size_t i = block_begin + 1; i < block_end; i++) {
                sums[i] += value * s;
                lazy_markers[i] += value;
                maxs[i] += value;
                mins[i] += value;
            }
        }

    //与query和update相同的结构：是否在同一块内->计算，query_min同理
    T query_max(size_t begin, size_t end) {
        size_t block_begin = begin / s;
        size_t block_end = end / s;

        T max_val = numeric_limits<T>::min();

        if(block_begin == block_end) {
            for(size_t i = begin; i <= end; i++) {
                max_val = max(max_val, datas[i] + lazy_markers[block_begin]); //注意处理懒惰标记的影响，以下同理
            }
            return max_val;
        }

        for(size_t i = begin; i < (block_begin + 1) * s; i++) {
            max_val = max(max_val, datas[i] + lazy_markers[block_begin]);
        }

        for(size_t i = block_end * s; i <= end; i++) {
            max_val = max(max_val, datas[i] + lazy_markers[block_end]);
        }

        for(size_t i = block_begin + 1; i < block_end; i++) {
            max_val = max(max_val, maxs[i]);
        }

        return max_val;
    }

    T query_min(size_t begin, size_t end) {
        size_t block_begin = begin / s;
        size_t block_end = end / s;

        T min_val = numeric_limits<T>::max();

        if(block_begin == block_end) {
            for(size_t i = begin; i <= end; i++) {
                min_val = min(min_val, datas[i] + lazy_markers[block_begin]);
            }
            return min_val;
        }

        for(size_t i = begin; i < (block_begin + 1) * s; i++) {
            min_val = min(min_val, datas[i] + lazy_markers[block_begin]);
        }

        for(size_t i = block_end * s; i <= end; i++) {
            min_val = min(min_val, datas[i] + lazy_markers[block_end]);
        }

        for(size_t i = block_begin + 1; i < block_end; i++) {
            min_val = min(min_val, mins[i]);
        }

        return min_val;
    }
};

一般而言，不会有题目同时要求进行数据变更、求区间和、求最值。

如果有，更推荐写线段树，毕竟分块拓展到这种程度也不简单了。

最后，对于懒惰标记的影响范围：

  • 赋值时：由update方法确定区间和的懒惰标记（datas、maxs、mins；不完整块直接线性增加）。
  • 使用时：只对完整区间内的datas（换句话说，第三个循环/遍历中间块的循环内的datas）数据增加该块的懒惰标记；在query、query_max、query_min内使用。

例题

如上文，几乎没有同时要求进行数据变更、求区间和、求最值的例题。

这里随便放一道看看得了。

题目来自洛谷P1816 忠诚

题目描述

老管家是一个聪明能干的人。他为财主工作了整整1010年。财主为了让自已账目更加清楚，要求管家每天记kk次账。由于管家聪明能干，因而管家总是让财主十分满意。但是由于一些人的挑拨，财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚，他把每次的账目按1,2,3,...1,2,3,...编号，然后不定时的问管家问题，问题是这样的：在aa到bb号账中最少的一笔是多少？为了让管家没时间作假，他总是一次问多个问题。

输入格式

输入中第一行有两个数m,nm,n表示有mm笔账和nn个问题。

第二行为mm个数，分别是账目的钱数。

后面nn行分别是nn个问题，每行有22个数字说明开始结束的账目编号。

输出格式

在一行中输出每个问题的答案，以一个空格分割。

输入样例

1
2
3
4
5
10 3
1 2 3 4 5 6 7 8 9 10
2 7
3 9
1 10

输出样例

1
2 3 1

题解

上文重复了多遍建块以及各种操作的代码，故而这里只给出main函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;

//blocks相关

int main() {
    int m, n;
    cin >> m >> n;
    vector<int> data(m);
    for(int i = 0; i < m; ++i) {
        cin >> data[i];
    }

    blocks<int> b(data, size_t(sqrt(data.size())));

    vector<int> results;
    for(int i = 0; i < n; ++i) {
        int a, c;
        cin >> a >> c;
        results.push_back(b.query_min(a - 1, c - 1));
    }

    for(int result : results) {
        cout << result << " ";
    }
    cout << endl;

    return 0;
}

补充

再次申明：分块是一种思想而不是数据结构，故而用法绝对不止这些。

在同时处理大量数据时，不妨考虑一下分块。

线段树

线段树是用来维护区间信息的数据结构。

相比于分块而言，线段树的结构更为细化，可以精确的控制数据的索引范围，而无需对于不完整部分进行遍历。

原理

线段树将每个长度不为11的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。
——OI WIKI - 线段树

看到这段话之后有没有想起什么？

没错，是递归。通过递归就可以不断细化每一个左、右子树，直至叶节点为止。

建树

首先建立数据结构：

1
2
3
4
5
6
template <class T>
class SegTree {
	vector<T> datas;
	vector<T> lazy_markers; //懒惰标记，应该没忘记吧
	size_t length;
};

然后考虑递归建树即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//是SegTree的成员函数
void build(vector<T> &d, size_t node, size_t begin, size_t end) {
	if(begin == end) { //是叶节点
		datas[node] = d[begin];
	}
	else { //不是叶节点
		size_t mid = (begin + end) / 2;
		build(d, node * 2 + 1, begin, mid);    //左子树
		build(d, node * 2 + 2, mid + 1, end);  //右子树
		datas[node] = datas[node * 2 + 1] + datas[node * 2 + 2];
	}
}

public:
	SegTree(vector<T> &d) { //构造函数
		datas.clear();
		lazy_markers.clear();
		length = d.size();

		datas.resize(length * 4);
		lazy_markers.resize(length * 4, 0);

		build(d, 0, 0, length - 1);
	}

可能会有人认为完全二叉树的左右子节点应该是2n2n与2n+12n+1，但对于0base的数组而言，显然2×0=02\times 0=0代表不了子节点。

查询/区间和

为何线段树由于分块？答案就在这里。

来看看这张图（备好草稿纸，照着下面的流程对着图自己想象一下）：

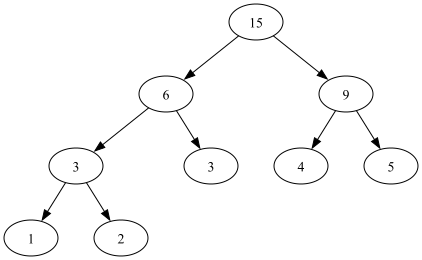
根据build方法，对{1, 2, 3, 4, 5}建树，可以得到这样的一棵完全二叉树。

若我们希望得到[b,e]\left[ b,e\right]的区间和，流程如下：

    1. 将目前区间[s,t]\left[ s,t\right]设置为整个区间；
    1. 目前区间是[b,e]\left[ b,e\right]的子区间吗？如果是，返回目前区间的区间和；如果不是且[b,e]\left[ b,e\right]与目前区间有交区间，继续。
    1. mid=s+t2mid=\frac{s+t}{2}，由此将目前区间划分为左区间（左子树；右子树同理）[s,mid]\left[ s,mid\right]与右区间[mid+1,t][mid+1,t]；
    1. 递归查找左区间与右区间，返回左区间返回值与右区间返回值之和。

这样可以方便快速地将待查区间划分为尽可能大的不同区间，而这些区间的区间和已经被储存，就不需要遍历以获取区间和了。

代码如下：

1
2
3
4
5
6
7
8
9
10
//是SegTree的成员函数
T query(size_t node, size_t begin_now, size_t end_now, size_t begin, size_t end) {
	if(begin_now > end || end_now < begin) return 0; //不在查找范围内，返回0
	if(begin_now >= begin && end_now <= end) return datas[node]; //目前区间是目标区间的子区间，返回区间和

	size_t mid = (begin_now + end_now) / 2;
	T left_res = query(node * 2 + 1, begin_now, mid, begin, end);       //左区间
	T right_res = query(node * 2 + 2, mid + 1, end_now, begin, end);  //右区间
	return left_res + right_res;
}

调用时使用this->query(0, 0, length - 1, b, e)即可。

修改

利用懒惰标记即可，这里的懒惰标记表明“这个区间内的所有元素都应当加上懒惰标记”。

换句话说，你会发现懒惰标记与线段树的大小与结构一模一样。对于节点node，其懒惰标记就存在lazy_markers[node]里。

因此流程实际上与求区间和是一模一样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//是SegTree的成员函数
void update(size_t node, size_t begin_now, size_t end_now, size_t begin, size_t end, T value) {
	if(begin_now > end || end_now < begin) return;
	if(begin_now >= begin && end_now <= end) {
		datas[node] += (end_now - begin_now + 1) * value; //区间和增加
		if(begin_now != end_now) {
			lazy_markers[node * 2 + 1] += value; //设置左右区间的懒惰标记（即整个区间）
			lazy_markers[node * 2 + 2] += value;
		}
		return;
	}

	size_t mid = (begin_now + end_now) / 2;
	update(node * 2 + 1, begin_now, mid, begin, end, value);          //左区间
	update(node * 2 + 2, mid + 1, end_now, begin, end, value);      //右区间
	datas[node] = datas[node * 2 + 1] + datas[node * 2 + 2]; //当前区间
}

为了应用懒惰标记，我们也需要一个方法，这个方法将当前节点的懒惰标记加载当前节点的值上，然后设置其左右子节点的懒惰标记（传递懒惰标记）

那就写呗：

1
2
3
4
5
6
7
8
9
10
11
//是SegTree的成员函数
void push(size_t node, size_t begin_now, size_t end_now) { //在使用时传递区间大小
	if(lazy_markers[node] != 0) { //需要更新
		datas[node] += (end_now - begin_now + 1) * lazy_markers[node];
		if(begin_now != end_now) { //不是叶节点
			lazy_markers[2 * node + 1] += lazy_markers[node];
			lazy_markers[2 * node + 2] += lazy_markers[node];
		}
		lazy_markers[node] = 0; //释放
	}
}

你会发现这个操作是O(1)O\left(1 \right)的。

Without thinking twice，在每次query与update以前调用即可。

比较

不像分块那么复杂，只需要修改维护datas的规则，我们就可以轻松进行对最小/最大值的查询。

当前对datas的维护规则是：datas[i]=datas[2i+1]+datas[2i+2]datas\left[i \right]=datas\left[2i+1 \right]+datas\left[2i+2 \right]，将sum改为min或者max即可得到最值。（懒惰标记的维护不变）

代码就不放了。

例题

来一道模板吧！

题目来自洛谷P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

  • 将某区间每一个数加上kk。
  • 求出某区间每一个数的和。

输入格式

第一行包含两个整数m,nm,n，分别表示该数列数字的个数和操作的总个数。

第二行包含nn个用空格分隔的整数，其中第ii个数字表示数列第ii项的初始值。

接下来mm行每行包含33或44个整数，表示一个操作，具体如下：

  • 1 x y k 将区间[x,y]\left[ x,y\right]内每个数加上kk
  • 2 x y 输出区间[x,y]\left[ x,y\right]内每个数的和

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入样例

1
2
3
4
5
6
7
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例

1
2
3
11
8
20

题解

套！！！模！！！板！！！

注！！！意！！！开！！！long long！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include <bits/stdc++.h>
using namespace std;

template <class T>
class SegTree {
	vector<T> datas;
	vector<T> lazy_markers;
	size_t length;
	
	void build(vector<T> &d, size_t node, size_t begin, size_t end) {
    	if(begin == end) {
    		datas[node] = d[begin];
    	}
    	else {
    		size_t mid = (begin + end) / 2;
    		build(d, node * 2 + 1, begin, mid);
    		build(d, node * 2 + 2, mid + 1, end);
    		datas[node] = datas[node * 2 + 1] + datas[node * 2 + 2];
    	}
    }
    
    T query(size_t node, size_t begin_now, size_t end_now, size_t begin, size_t end) {
        push(node, begin_now, end_now);
        if(begin_now > end || end_now < begin) return 0;
        if(begin_now >= begin && end_now <= end) return datas[node];

        size_t mid = (begin_now + end_now) / 2;
        T left_res = query(node * 2 + 1, begin_now, mid, begin, end);
        T right_res = query(node * 2 + 2, mid + 1, end_now, begin, end);
        return left_res + right_res;
    }
    
    void update(size_t node, size_t begin_now, size_t end_now, size_t begin, size_t end, T value) {
        push(node, begin_now, end_now);
        if(begin_now > end || end_now < begin) return;
        if(begin_now >= begin && end_now <= end) {
            datas[node] += (end_now - begin_now + 1) * value;
            if(begin_now != end_now) {
                lazy_markers[node * 2 + 1] += value;
                lazy_markers[node * 2 + 2] += value;
            }
            return;
        }

        size_t mid = (begin_now + end_now) / 2;
        update(node * 2 + 1, begin_now, mid, begin, end, value);
        update(node * 2 + 2, mid + 1, end_now, begin, end, value);
        datas[node] = datas[node * 2 + 1] + datas[node * 2 + 2];
    }
    
    void push(size_t node, size_t begin_now, size_t end_now) {
        if(lazy_markers[node] != 0) {
            datas[node] += (end_now - begin_now + 1) * lazy_markers[node];
            if(begin_now != end_now) {
                lazy_markers[2 * node + 1] += lazy_markers[node];
                lazy_markers[2 * node + 2] += lazy_markers[node];
            }
            lazy_markers[node] = 0;
        }
    }
    
    public:
    	SegTree(vector<T> &d) {
    		datas.clear();
    		lazy_markers.clear();
    		length = d.size();
    
    		datas.resize(length * 4);
    		lazy_markers.resize(length * 4, 0);
    
    		build(d, 0, 0, length - 1);
    	}
    	
    	void update(size_t l, size_t r, T value) {
            update(0, 0, length - 1, l, r, value);
        }

        T query(size_t l, size_t r) {
            return query(0, 0, length - 1, l, r);
        }
};

int main() {
    long long n, m;
    cin >> n >> m;

    vector<long long> data(n);
    for(long long &in : data) {
        cin >> in;
    }

    SegTree<long long> tree(data);

    for(long long turn = 0; turn < m; turn++) {
        long long opt;
        cin >> opt;

        if(opt == 1) {
            long long x, y, k;
            cin >> x >> y >> k;
            x--;
            y--;
            tree.update(x, y, k);
        } else {
            long long x, y;
            cin >> x >> y;
            x--;
            y--;
            cout << tree.query(x, y) << endl;
        }
    }

    return 0;
}

题外话

把全站所有小节标题由h3改成h2了，其它依次上升。

主要是h5比正文还小了。

以及总算是一知半解（？）地弄会了线段树。

这下可以做绿题（？）了哈哈。

注释

  1. 本文内的除法均为整数除法。 ↩
编程
#计算机 #编程 #cpp
学习笔记——分块、线段树
https://www.ordchaos.com/posts/6e841aef/
作者
序炁
发布于
2024年8月5日
许可协议